벡터 연산은 3D 그래픽, 물리, 애니메이션이 기본이 되며, Unity을 잘 활용하려면 이것을 깊이 있게 이해하면 매우 유용합니다. 다음은 주요 연산자에 대한 설명과 이들이 사용될 수 있는 많은 것들에 대한 제안사항을 보여줍니다.

두 개의 벡터를 덧셈하면, 그 결과는 원래의 벡터를 "계단(steps)"으로 하나씩 차례로 더하는 것과 같습니다. 두 변수의 순서는 그 결과가 어느 순서이든 같으므로 상관하지 않습니다.

만일 첫 번째 벡터가 공간에서 한 점으로 자리한다면, 두 번째는 첫 번째로부터의 오프셋이나 "jump"로 해석됩니다. 예를 들어, 지상의 한 지점에서 위로 5 단위 위에 있는 점을 찾으려면, 다음과 같은 계산을 사용할 수 있습니다:-

var pointInAir = pointOnGround + new Vector3(0, 5, 0);

만일 그 벡터가 힘을 나타내면, 그것의 방향과 크기의 관점에서 생각하는 것이 더 직관적입니다(크기(magnitude)란 힘의 크기를 말합니다). 두 개의 벡터를 더하게 되면 두 힘의 합산과 동일한 새로운 벡터가 생성됩니다. 이런 개념은 여러 개의 별개의 컴포넌트가 가진 힘을 한꺼번에 적용할 때 종종 유용합니다(예: 앞으로 추진하는 로켓도 옆 바람의 영향을 받을 수 있습니다).

벡터의 뺄셈은 한 오브젝트에서 다른 오브젝트로 방향과 거리를 얻을 때 가장 많이 사용됩니다. 두 매개변수의 순서는 뺄셈에서는 의미가 있음을 기억합니다:-

//벡터 d는 c와 같은 크기를 가지지만 방향은 반대입니다.
var c = b - a;
var d = a - b;

숫자와 마찬가지로, 벡터의 음수를 덧셈하는 것은 양수를 뺄셈하는 것과 같습니다.

//이 둘은 같은 결과를 제공합니다.
var c = a - b;
var c = a + -b;

벡터의 음수는 원래 것과 같은 크기를 가지며, 같은 라인을 따라 정확히 반대방향을 가리킵니다.

벡터를 논 할 때, 일반적인 숫자(예: 부동 값)을 스칼라 라고 말하는 것이 보통입니다. 이것의 의미는 스칼라는 "크기"나 규모만 있는 반면에, 벡터는 크기와 방향을 모두 가지고 있습니다.

하나의 벡터를 스칼라로 곱하면 원래와 같은 방향을 가리키는 벡터라는 의미입니다. 하지만, 새 벡터의 크기는 원래 크기에 스칼라 값을 곱한 것과 같습니다.

마찬가지로, 스칼라의 나눗셈은 원래 벡터의 크기를 스칼라로 나눈 것 입니다.

이 연산은 벡터가 움직임의 오프셋이나 힘을 나타낼 경우 유용합니다. 여기서는 방향에 영향을 주지 않고 벡터의 크기만 변경할 수 있게 해 줍니다.

어떤 벡터가 자신의 크기로 나눌 경우, 그 결과는 크기 1의 벡터가 되며, 이것은 정규화된(normalized) 벡터라고 합니다. 만일 정규화된 벡터에 스칼라를 곱하면, 그 결과의 크기는 스칼라의 값과 같습니다. 이것은 어떤 힘의 방향은 일정하나 그 힘을 조절할 수 있을 때 유용합니다(예: 자동차 바퀴에서 오는 힘은 항상 앞쪽으로 향하지만 그 힘은 운전자에 의해 제어되는 경우).

벡터의 내적(dot product)은 두 개의 벡터로 계산하여 스칼라를 반환합니다. 여기서 스칼라는 두 벡터의 힘을 서로 곱하여 그 결과를 두 벡터 간의 각도의 코사인(cosine)으로 곱한 것과 같습니다. 두 벡터가 정규화되면, 이 코사인은 본질적으로 첫 번째 벡터가 두 번째 벡터 내에서 얼마나 뻗어가는 가를 말해줍니다(혹은 그 변수의 반대 순서로 계산해도 상관없습니다).

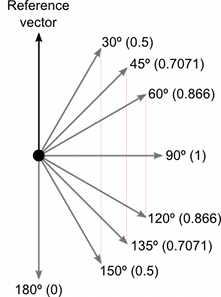
각도의 관점에서 생각하는 만큼 쉬우며 계산기를 사용하여 해당하는 코사인을 찾으면 됩니다. 하지만, 다음 도표에서 보여준 대로 일부 주요 코사인 값에 대해 직관적으로 이해하면 유용합니다:-

벡터의 내적(dot product)은 Mathf.Cos 함수 대신 사용하거나 어떤 상황에서 벡터 크기의 연산에 사용될 수 있는 매우 쉬운 연산입니다(이 둘은 정확하게 같은 것을 하는 것은 아니지만 때에 따라 그 효과는 동일합니다). 하지만, 벡터의 내적 함수의 계산은 CPU 시간을 훨씬 덜 소모하므로 귀중한 최적화가 될 수 있습니다.

다른 연산들은 2D와 3D, 그리고 다른 수의 차원에서의 벡터를 정의되었습니다. 벡터의 외적(Cross Product)은 이와 반대로, 3D 벡터에서만 의미를 가집니다. 이것은 두 벡터를 입력으로 받아 그 결과로 다른 벡터를 반환합니다.

그 결과 벡터 값은 두 입력 벡터와 수직이 됩니다. 두 개의 입력 벡터의 순서에서 출력 벡터의 방향을 찾아내는 "왼손의 법칙"이 유용할 수 있습니다. 만일 첫 매개 변수가 손의 엄지손가락과 일치한다면, 두 번째 매개변수는 집게손가락과 일치하고, 그리고 그 결과값은 가운데 손가락의 방향을 가리킬 것 입니다. 만일 이 매개변수들의 순서가 반대라면, 그 결과 벡터는 같은 크기를 가지지만 정확하게 반대방향을 가리킬 것입니다.

이 결과의 크기는 입력 벡터들의 크기를 서로 곱한 후, 그 값을 그 둘 사이의 각도의 사인(sine) 값으로 곱셈한 것과 같습니다:-

벡터의 외적(Cross Product)은 그 결과 값을 위해 몇 가지 유용한 부분을 합치기 때문에 일견 복잡해 보입니다. 하지만, 벡터의 내적(Dot Product)과 마찬가지로, 이는 훨씬 느린 초월 함수에 의존하는 것보다는 수학적으로 매우 효율적입니다.

• 출처: 유니티코리아위키 (CC BY-NC-SA 2.0)